Number Systems and Radix Conversion

Number Systems and Radix Conversion ALSU is a combinational circuit so inside an ALSU, we have AND, OR, NOT and other different gates combined together in different ways to perform addition, subtraction, and,
or, not, etc. Up till now, we consider ALSU as a “black box” which takes two operands, a and b, at the input and has c at the output. Control signals whose values depend upon the opcode of an instruction were associated with this black box.
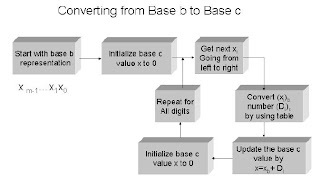
In order to understand the operation of the ALSU, we need to understand the basis of the representation of the numbers. For example, a designer needs to specify how many bits are required for the source operands and how many will be needed for the destination operand after an operation to avoid overflow and truncation. Radix Conversion Now we will consider the conversion of numbers from a representation in one base to another. As human works with base 10 and computers with base 2, this radix conversion operation is important to discuss here. We will use base c notion for decimal representation and base b for any other base. The following figure shows the algorithm of converting from base b to base c:

Example Convert the hexadecimal number B316 to base 10.
Solution
According to the above algorithm,
X=0
X= x+B (=11) =11
X=16*11+3= 179
Hence B316=17910
The following figure shows the algorithm of converting from base c to base b: